Ted Wang a master of none
Dijkstra's Algorithm - Java Implementation

Graph problem is often one of the most difficult problems in computer science. Problems that we might encounter with graphs are: graph connectivity, maximum network flow, minimum spanning tree, finding the shortest path, etc…
Let’s talk about finding the shortest path in this blog. The most commonly used algorithm to find the shortest path or longest path is Dijkstra’s Algorithm. Dijkstra’s shortest path algorithm was conceived by computer scientist Edsger W. Dijkstra in 1956. It is a greedy algorithm with time complexity of O(|V| + |E|)log(|V|).
Algorithm summary
The algorithm is actually pretty easy to understand. We use a queue to visit each node. We enqueue the first starting node to the queue, and visit all his children. While visiting all children, we keep track the shortest path from the starting node to this current child. We also update the previous node that we used to reach to this child. When all children for this node are visited, we mark the current node as visited. This process is repeated until the destination node is found or all nodes are visited (there is no path to reach the destination).
Pseudocode
Here is the pseudocode for Dijkstra’s algorithm (reference to Dijkstra’s algorithm)
1 function Dijkstra(Graph, source):
2
3 create vertex set Q
4
5 for each vertex v in Graph:
6 dist[v] ← INFINITY
7 prev[v] ← UNDEFINED
8 add v to Q
9 dist[source] ← 0
10
11 while Q is not empty:
12 u ← vertex in Q with min dist[u]
13
14 remove u from Q
15
16 for each neighbor v of u: // only v that are still in Q
17 alt ← dist[u] + length(u, v)
18 if alt < dist[v]:
19 dist[v] ← alt
20 prev[v] ← u
21
22 return dist[], prev[]
Sample Problem
Here is a sample example that I created to test our algorithm. We have a graph consists of node A, B, C, D, with edges shown below:
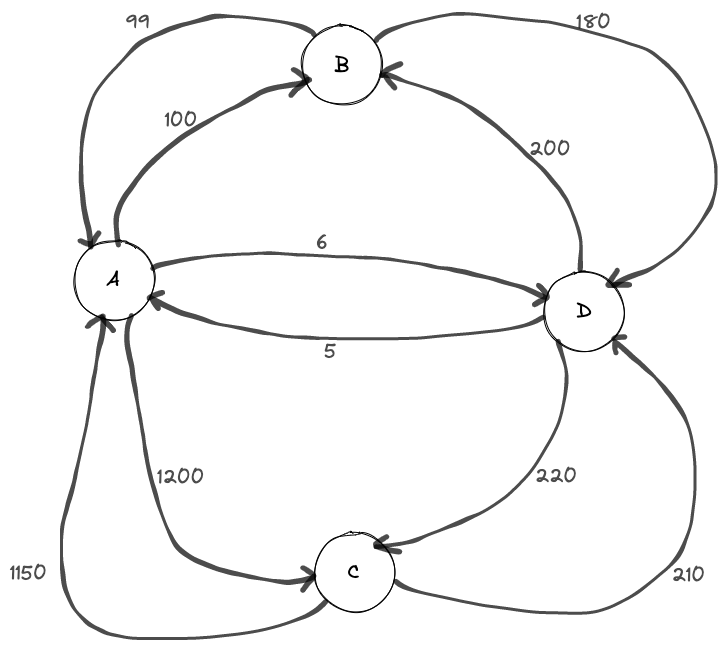
Let’s say we want to find the shortest path from B to C. The shortest path is 325 and the trajectory is showed below in green:
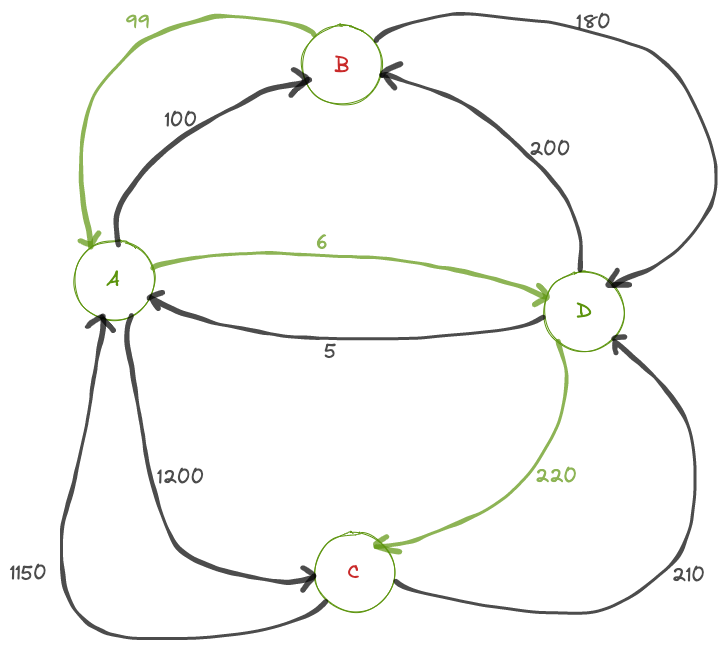
Java Implementation
Here is my quick implementation for Dijkstra’s algorithm using Java. Let’s have a Node class to store the shortest path and previous node. We will initiate the shortest path by maximum integer value.
public class Node {
int shortestPath;
Node previousNode;
String val;
public Node(String val) {
this.val = val;
shortestPath = Integer.MAX_VALUE;
previousNode = null;
}
}
Now, let’s implement the Graph class. We need several functions for this class. Firstly, we need a function buildGraph()
to build the input to a graph. I also implemented a printGraph() function since I am a visual person and need to verify
the graph. We need a function dijkstra() to implement Dijsktra’s algorithm. Finally, a function printPath() to print
the shortest path.
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Set;
public class Graph {
Map<String, Node> allNodes;
Map<Node, Map<Node, Integer>> graph;
public Graph() {
allNodes = new HashMap<>();
graph = new HashMap<>();
}
public void buildGraph(Map<String, Map<String, Integer>> relations) {
for (String pair : relations.keySet()) {
String first = pair.split("-")[0];
String second = pair.split("-")[1];
Map<String, Integer> edgeToChildren = relations.get(pair);
Integer fromFtoS = edgeToChildren.get("firstToSecond");
Integer fromStoF = edgeToChildren.get("secondToFirst");
allNodes.put(first, allNodes.getOrDefault(first, new Node(first)));
allNodes.put(second, allNodes.getOrDefault(second, new Node(second)));
graph.put(allNodes.get(first), graph.getOrDefault(allNodes.get(first), new HashMap<>()));
graph.put(allNodes.get(second), graph.getOrDefault(allNodes.get(second), new HashMap<>()));
graph.get(allNodes.get(first)).put(allNodes.get(second), fromFtoS);
graph.get(allNodes.get(second)).put(allNodes.get(first), fromStoF);
}
}
public void printGraph() {
System.out.println("The graph has the following structure:");
graph.keySet().stream().forEach(node -> {
System.out.print(node.val + ": ");
graph.get(node).keySet().stream().forEach(
child -> {
System.out.print("(" + child.val + ", " + graph.get(node).get(child) + ") ");
});
System.out.println();
});
System.out.println();
}
public int dijkstra(String[] verticesPair) {
String start = verticesPair[0];
String goal = verticesPair[1];
Set<String> visited = new HashSet<>();
Queue<Node> q = new LinkedList<>();
allNodes.get(start).shortestPath = 0;
q.add(allNodes.get(start));
while(!q.isEmpty()) {
Node cur = q.poll();
PriorityQueue<Node> children = new PriorityQueue<>((a, b) -> (graph.get(cur).get(a) - graph.get(cur).get(b)));
for (Node child : graph.get(cur).keySet()) {
children.add(child);
}
for (Node child : children) {
if (visited.contains(child.val)) continue;
if (child.shortestPath > cur.shortestPath + graph.get(cur).get(child)) {
child.shortestPath = cur.shortestPath + graph.get(cur).get(child);
child.previousNode = cur;
}
q.offer(child);
}
visited.add(cur.val);
}
return allNodes.get(goal).shortestPath;
}
public void printPath(String start, String goal) {
Node node = allNodes.get(goal);
List<Node> path = new ArrayList<>();
while (node.previousNode != null) {
if (node == allNodes.get(start)) break;
path.add(node);
node = node.previousNode;
}
path.add(node);
Collections.reverse(path);
path.stream().forEach(n -> {
if (n == allNodes.get(goal)) System.out.println(n.val);
else System.out.print(n.val + " --> ");
});
System.out.println();
}
}
Validation
Now, let’s validate the Dijkstra’s algorithm with the example that we showed above.
public class ShortestPath {
public static void main(String[] args) {
Map relations = Map.of(
"A-B", Map.of("firstToSecond", 100, "secondToFirst", 99),
"A-C", Map.of("firstToSecond", 1200, "secondToFirst", 1150),
"D-B", Map.of("firstToSecond", 200, "secondToFirst", 180),
"D-C", Map.of("firstToSecond", 220, "secondToFirst", 210),
"A-D", Map.of("firstToSecond", 6, "secondToFirst", 5)
);
Graph graph = new Graph();
graph.buildGraph(relations);
graph.printGraph();
System.out.println("Shortest path from B-C is: " + graph.dijkstra(new String[]{"B", "C"}));
System.out.println();
System.out.println("The shortest path from B to C is: ");
graph.printPath("B", "C");
}
}
The graph that we build using graph.printGraph() is shown below. It is the correct graph structure that presents the above example.
The graph has the following structure:
C: (D, 210) (A, 1150)
B: (D, 180) (A, 99)
D: (C, 220) (B, 200) (A, 5)
A: (C, 1200) (B, 100) (D, 6)

Now, let’s run graph.dijkstra(new String[]{"B", "C"}) and graph.printPath("B", C") to see the shortest path and its
trajectory.
Shortest path from B-C is: 325
The shortest path from B to C is:
B --> A --> D --> C

The shortest path is 325, and the path trajectory aligns with our expectation. Here you go. This is my simple Java implementation of the Dijkstra’s algorithm. I hope this helps you to understand better the algorithm and also how to implement it.
Written on June 3rd , 2021 by Ted Wang